Right triangles with regular features, or for which simple formulas exist, are called special right triangles. As an example, a right triangle may have angles that have simple relationships, such as 45°–45°–90°. These are referred to as “angle-based” right triangles. When the sides of the right triangle form ratios, such as 3: 4: 5, or other special ratios, such as the golden ratio, there is a right triangle that is “side-based”. It is easier to solve geometric problems without resorting to more complex methods if one knows the relationships between the angles or ratios of sides of these special triangles.
Understanding Special Right Triangles:
If you are able to recognize special right triangles, it can prove useful when answering some geometry questions. A special right triangle is a right triangle in which the sides are in a particular ratio, called the Pythagorean Triples. The Pythagorean theorem can also be used, but if you can recognize that this triangle is a special triangle then you can save yourself some calculations.
These figures show some examples of right triangles and Pythagorean triples. Please scroll down the page to find some explanations about right triangles, Pythagorean triples, videos and worksheets.
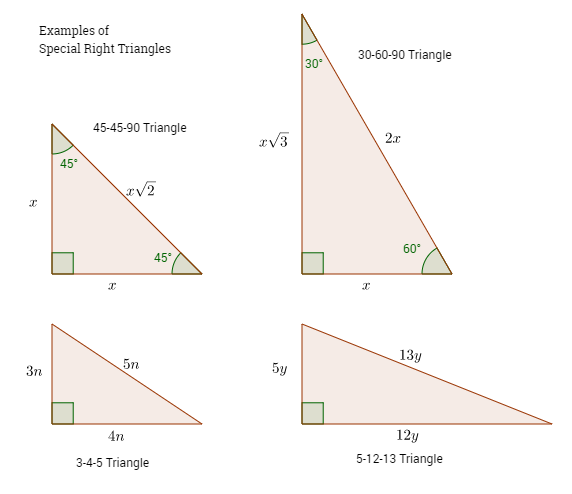
What is the 45°-45°-90° Triangle?
Triangles with 45°, 45° and 90° angles are called 45°-45°-90° triangles. The lengths of the sides of a triangle with 45°, 45° and 90° are in the ratio 1: 1: √2.
There is a right triangle with two sides of equal length that must be a 45°-45°-90° triangle.
The angles of a 45°-45°-90° triangle can also be viewed as a sign that it is a triangle. The right triangle that has a 45° angle must be a special right triangle that has a 45°-45°-90° angle.
Assume that Side 1: Side 2: Hypotenuse equals x: x: x√2.
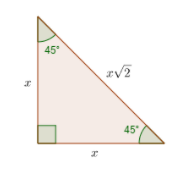
Example No 1:
It is possible to find the length of the hypotenuse of a right triangle if the lengths of the other two sides are both three inches long.
Solution:
Step 1: Since this is a right triangle with two equal sides, the triangle’s angles must be 45°-45°-90°.
Step 2: You are given that the dimensions of both sides are three. Suppose the first and second value of the ratio x:x:x√2 is 3 then the length of the third side will be 3√2.
Answer: The hypotenuse is 3√2 inches in length.
How does a triangle of 30°-60°-90° work?
It is possible to make other types of right triangles special as well, such as the 30°-60°-90° triangles. In this case we have a right triangle whose angles are 30°-60°-90°. A 30°-60°-90° triangle has sides in the ratio of 1: √3: 2 and a triangle with sides of 30°-60°-90° has sides in the ratio of 3: 2.
A triangle with an angle of 30°-60°-90° can also be recognized by its angle. The right-angle triangle is a special right triangle if one of the angles is either 30° or 60° in the right-angle triangle, then it must be a 30°-60°-90° right triangle. The right triangle that has a 30° angle or a 60° angle must be a 30°-60°-90° special right triangle.
The Hypotenuse = x: x√3: 2x

Example No 1:
You can calculate the length of the hypotenuse of a right triangle if the lengths of the other two sides are 4 inches and 4 inches and 3 inches, respectively.
Solution:
Step 1: Look at the ratio of the lengths to see if it matches the n: n√2:2n ratio.
4:4√3? = x:x√3:2x
Step 2: Yes, it is a 30°-60°-90° triangle for x = 4
Step 3: Calculate the third side.
2x = 2 × 4 = 8
Answer: The Hypotenuse measures 8 inches long.
